必要条件、十分条件

「必要条件」「十分条件」の知識は論理的な文章を書く手助けになる

数学で学習した「必要条件」と「十分条件」を知っていれば、論理的な文章を書く手助けになります。そこで、このページでは、必要条件、十分条件を、わかりやすく解説します。

なお、このページは、数学が苦手な人に向けて書いています。
数学が嫌いな人こそ、このページを読んでくださいね。

必要条件、十分条件を難しく説明

必要条件、十分条件とは、一言でいえば、以下です。

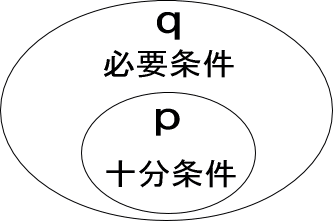
「pならばq」の命題が真のとき、pはqの十分条件、qはpの必要条件である

これをそのまま理解できれば、すでに、必要条件、十分条件のことがわかっているということなので、このページは読み飛ばしてください。

「何のことかよくわからない」と思っている人だけ、以下を読み進めてください。

命題とは？

正しいか、正しくないかが明確に決まるもののことを「命題」と言います。
命題が正しいことを真、正しくないことを偽であるといいます。

（例）彼は背が高い
本当に背が高いかもしれませんが、どのくらい背が高いのか明確ではありません。だから、この例は命題ではありません。

（例）彼の身長は180センチです。
身長が180センチかどうか、明確にわかります。だから、この例は命題です。仮に彼の身長を測定して、170センチしかなければ「偽」、180センチならば「真」になります。

十分条件とは？

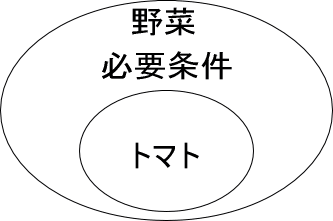
「野菜」と「トマト」の関係を考えてみましょう。
野菜とトマトの関係を図で表すと、下記の（ア）と（イ）のうち、どちらになると思いますか。



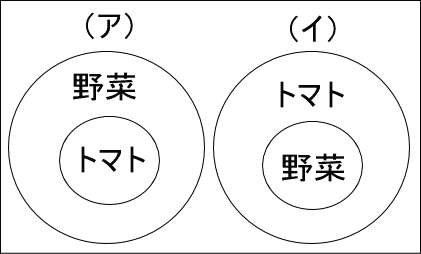
もちろん、（ア）ですよね。
なぜなら、ピーマン、ニンジン…色々ある野菜の中に、トマトがあるためです。



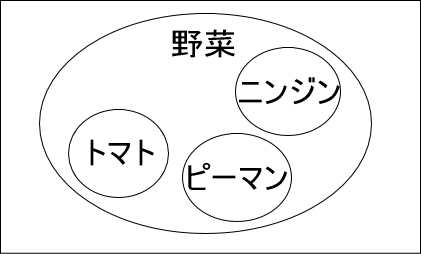
さて、ここで、上図のトマトに着目してください。

トマトは、野菜ですね。
トマトならば、野菜。
このようなとき、トマトは（野菜であるための）十分条件といいます。

必要条件

野菜に着目してください。



野菜といえば、トマトですか？
違いますよね。
他にも、ニンジンやピーマンなどの野菜がありますので、野菜といえば、トマトではありません。

つまり、「野菜」と「トマト」の関係は、「野菜といえばトマトではない（トマト以外にも野菜はある）」ということになります
このようなとき、野菜は（トマトであるための）必要条件といいます。

必要条件と十分条件

必要条件、十分条件、何かややこしいですよね。
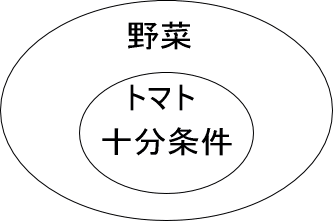
下図を見て、必要条件か十分条件か埋めることができますか？



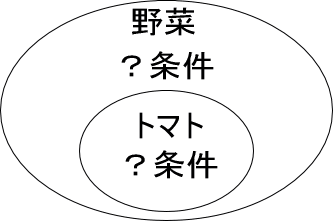
この図、どのように考えるのかというと以下です。

・十分条件：「そう言うのに十分」だと覚えておく

まずは、トマトに注目してください。
仮に、正体不明のAがあったとします。
「Aはトマト」といえば、「Aは野菜」であるといえますよね。
言い換えると、Aがトマトとさえ言えば、野菜だと十分にいえます。
だから、図の内側は十分条件になります。

・必要条件：「そうかもしれないけど、それだけではない」と覚えておく

次に、野菜に注目してください。
仮に、正体不明のAがあったとします。
「Aが野菜」というだけでは、「Aはトマト」とはいえませんよね。確かにAがトマトである確率もありますが、野菜にはトマト以外もあるため、必ずしもそういうことができません。
言い換えると、Aが野菜といえば、トマトかもしれないけど、それだけではないといえます。
だから、図の外側は、必要条件になります。

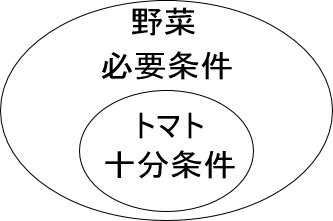
必要条件か十分条件（まとめ）

pならばqが真ならば、以下です。

・ｐはｑであるための十分条件
・ｑはｐであるための必要条件